- π to stosunek obwodu koła do jego średnicy.
- π to pole powierzchni koła o promieniu 1.
- π to połowa obwodu koła o promieniu 1.
- π to 1/4 pola powierzchni sfery o promieniu 1.
- π to 3/4 objętości kuli o promieniu 1.
- kπ dla całkowitych k to miejsca zerowe funkcji sinx.
- … i wiele innych …
Z OKAZJI ŚWIATOWEGO DNIA LICZBY π (PI) PRZEDSTAWIAMY KILKANAŚCIE (DOKŁADNIE 3 I 14, A WIĘC 17)
NIEZWYKŁYCH HISTORII, ZWIĄZANYCH Z π,
KTÓRĄ WIELU ŚMIAŁO ZWIE KRÓLOWĄ LICZB.
- Co ma wspólnego Dzień π z bombą atomową?
- Ile wynosi π według Biblii?
- Dlaczego π nazywa się π?
- Który z wzorów zawierających π jest najpiękniejszy?
- Czy starożytni Egipcjanie znali π?
- Kto jest patronem dnia π?
- Ile dokładnie wynosi wartość π?
- Kto wyliczył najwięcej cyfr π po przecinku?
- Kto miał największego pecha z powodu π?
- Po co wylicza się π z coraz większą dokładnością?
- Kto dostał Nagrodę Nobla za π?
- Czy można wykreślić odcinek długości π tylko z użyciem cyrkla i linijki?
- Czego jeszcze nie wiemy o π?
- Kto ma wyryte π na nagrobku?
- Kto jest autorem najsłynniejszego pi-ematu?
- Kto jest autorem najdłuższego pi-ematu?
- Kto z pamięci wyrecytował najwięcej cyfr π?
Święto π wymyślono i pierwszy raz obchodzono w roku 1988 w San Francisco w tamtejszym Exploratorium, pierwszym centrum nauki na świecie, w którym nie trzeba było ściszać głosu, eksponaty można było dotykać, przestawiać, a nawet zepsuć. Exploratorium stworzył Frank Oppenheimer, fizyk, brat Roberta Oppenheimera, który był szefem programu budowy pierwszej bomby atomowej na świecie.
Biblia, trzeba przyznać, niestety, mocno myli się w tym względzie. Z liczbą π spotykamy się w opisie budowy świątyni króla Salomona: "Sporządził też kadź odlewną wyobrażającą morze, okrągłą, długości dziesięciu łokci od krawędzi do krawędzi (...), obwód zaś jej wynosił trzydzieści łokci" (Pierwsza Księga Królewska 7, 23). To oznacza, że zdaniem natchnionego autora Starego Testamentu kadź miała obwód 30 i średnicę 10 łokci, co - po podzieleniu - daje π=3. Dziś w szkole za taką odpowiedź dostalibyśmy jedynkę.
Niektórzy myślą, że grecka litera π nawiązuje do imienia Pitagorasa. Ale naprawdę pochodzi ona od greckiego słowa "perimetron" lub "periferia' (obwód, obrzeże). To oznaczenie pojawiło się w roku 1706 roku w rozprawie angielskiego matematyka Williama Jonesa pt. "Synopsis Palmariorum Matheseos" ("Nowe wprowadzenie do matematyki"), a weszło do powszechnego użytku, gdy zaczął je stosować od 1736 roku słynny matematyk Leonhard Euler.
To subiektywny wybór, ale naszym zdaniem nic nie przebije wzoru:
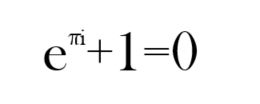
Jest on uznawany za najpiękniejszą formułę matematyczną - równość, dodawanie, mnożenie i potęgowanie wiąże ze sobą pięć kluczowych liczb: 0, 1, π, e oraz i (ta ostatnia wielkość to pierwiastek z minus 1, nazywa się jednostką urojoną).
Jakżeby inaczej - jest zakodowane w Wielkiej Piramidzie Cheopsa. Wzniesiono ją około 46 wieków temu w ten sposób, że obwód jej podstawy jest z dobrym przybliżeniem 2π razy większy niż jej wysokość. Tyle że... najprawdopodobniej był to zwykły przypadek. Ale jest lepszy dowód. W papirusie Ahmesa sprzed 36-39 wieków, uznawanym za jeden z najstarszych dokumentów matematycznych, gdzie wyliczane są m.in. różne objętości i pola powierzchni, w jednym z problemów można się dopatrzyć wyliczenia liczby π=3,1605, co nie jest bardzo złym przybliżeniem.
Najczęściej uznaje się, że Albert Einstein (1879-1955), ale czasem wymienia się naszego matematyka Wacława Sierpińskiego (1882-1969). Obaj uczeni urodzili się właśnie 14 marca.
Większość zadowala się odpowiedzią, że 3,14. Ale to oczywiście tylko wartość przybliżona. Dokładnej wartości podać nie sposób, bo π okazało się liczbą niewymierną (co udowodnił w 1767 roku szwajcarski matematyk Johann Lambert), a więc ciąg cyfr po przecinku będzie się ciągnął w nieskończoność, i to bez żadnych regularności. Można co najwyżej wypisać różne wzory na π, w których pojawią się nieskończone sumy czy iloczyny:

Wyjątkowo zgrabnym przybliżeniem liczby π jest ułamek 22/7.
Do 2016 roku rekord należał do anonimowego japońskiego programisty, który występował pod kryptonimem "houkouonchi". 8 października 2014 roku zakończył on komputerowe obliczenia, w których wyliczył aż 13,3 biliona cyfr dziesiętnego rozwinięcia π.
W listopadzie 2016 Peter Trueb uzyskał dokładność ok. 22,5 biliona miejsc po przecinku przy pomocy programu y-cruncher. Obliczenia zajęły 105 dni, a sama liczba zajęła ok. 120 TB miejsca. Niezależnie od algorytmów znajdujących coraz lepsze przybliżenia liczby pi opracowano metody obliczania pojedynczych bardzo odległych cyfr w rozwinięciu dziesiętnym liczby pi. Np. w roku 2010 obliczono cyfrę będącą na 2 000 000 000 000 000 miejscu po przecinku w rozwinięciu dziesiętnym liczby pi i wynosi ona zero. Obliczenia trwały 23 dni na 1000 maszynach.
Przed epoką komputerów obliczanie π było niezwykle żmudnym zadaniem. W 1874 roku angielski matematyk William Shanks po 30 latach pracy uroczyście ogłosił, że obliczył 707 cyfr π po przecinku. Jego wynik uchodził za rekordowy aż do 1944 roku, kiedy to inny angielski matematyk wykazał, że Shanks pomylił się na 528. miejscu i dalej już wszystkie podane przez niego cyfry były błędne. To znaczy, że ostatnie dziesięć lat życia Shanks mógł z powodzeniem spędzić na pożyteczniejszym zajęciu.
Wyłącznie dla sportu. Z punktu widzenia matematyki niczemu to nie służy. Nie ma to także żadnego praktycznego znaczenia. Znajomość już 47 miejsc po przecinku wystarcza, by wykreślić okrąg opisujący cały widoczny Wszechświat i nieróżniący się od doskonałego kształtu więcej niż o średnicę protonu.
Oczywiście Wisława Szymborska. Nasza poetka wysławiała π w jednym z wierszy z tomu "Wielka liczba":
Podziwu godna liczba Pi
trzy koma jeden cztery jeden.
Wszystkie jej dalsze cyfry też są początkowe,
pięć dziewięć dwa, ponieważ nigdy się nie kończy.
Nie pozwala się objąć sześć pięć trzy pięć spojrzeniem
osiem dziewięć obliczeniem
siedem dziewięć wyobraźnią,
a nawet trzy dwa trzy osiem żartem, czyli porównaniem
cztery sześć do czegokolwiek
dwa sześć cztery trzy na świecie.
Najdłuższy ziemski wąż po kilkunastu metrach się urywa
podobnie, choć trochę później, czynią węże bajeczne.
Korowód cyfr składających się na liczbę Pi
nie zatrzymuje się na brzegu kartki,
potrafi ciągnąć się po stole, przez powietrze,
przez mur, liść, gniazdo ptasie, chmury, prosto w niebo,
przez całą nieba wzdętość i bezdenność.
O, jak krótki, wprost mysi, jest warkocz komety!
Jak wątły promień gwiazdy, że zakrzywia się w lada przestrzeni!
A tu dwa trzy piętnaście trzysta dziewiętnaście
mój numer telefonu twój numer koszuli
rok tysiąc dziewięćset siedemdziesiąty trzeci szóste piętro
ilość mieszkańców sześćdziesiąt pięć groszy
obwód w biodrach dwa palce szarada i szyfr,
w którym słowiczku mój a leć, a piej
oraz uprasza się zachować spokój,
a także ziemia i niebo przeminą,
ale nie liczba Pi, co to to nie,
ona wciąż swoje niezłe jeszcze pięć,
nie byle jakie osiem,
nieostatnie siedem,
przynaglając, ach, przynaglając gnuśną wieczność
do trwania.
Niestety, nie. Niemiec Ferdinand Lindemann w roku 1882 udowodnił, że π jest liczbą przestępną, tzn. nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych. A to oznacza, że niemożliwa jest kwadratura koła, co się sprowadza do niemożności konstrukcji odcinka o długości π za pomocą linijki i cyrkla.
Pozostało jeszcze kilka zagadek, nad którymi się głowią matematycy. Na przykład nie wiadomo wciąż, czy liczbą przestępną jest ππ. Do dziś też nie wiemy, czy w nieskończonym ciągu rozwinięcia dziesiętnego π pojawia się zestaw cyfr 0123456789.
Holenderski matematyk Ludolph von Ceulen. Na przełomie XVI i XVII wieku wraz z żoną wyliczył 35 cyfr π, co było absolutnym rekordem, najdokładniejszą wartością w tamtych czasach. Wynik - 3,14159265358979323846264338327950288 - wyryto na jego nagrobku. Wyczyn ten sprawił, że liczbę π na jego cześć niegdyś nazywano ludolfiną.
Pi-ematy to wiersze (i teksty), które mają pomóc w zapamiętaniu jak największej liczby cyfr π. Zasada ich tworzenia jest prosta - liczba liter w kolejnych wyrazach tekstu odpowiada kolejnym cyfrom rozwinięcia dziesiętnego π. Prawdopodobnie pierwszy taki wierszyk powstał w pierwszej połowie XIX wieku po niemiecku. Najpopularniejszym polskim utworem szyfrującym 23 cyfry π jest wiersz Kazimierza Cwojdzińskiego, opublikowany w 1930 roku w czasopiśmie "Parametr":
Kuć i orać w dzień zawzięcie,
Bo plonów niema bez trudu!
Złocisty szczęścia okręcie,
Kołyszesz...
Kuć! My nie czekajmy cudu.
Robota to potęga ludu!
(Uwaga, "niema" pisało się wtedy razem!) Utworowi towarzyszył anons: "Autor prosi redakcję, by wezwała czytelników do napisania lepszego wiersza. Za najgładszy, elegancki i dowcipny wiersz autor powyższego wypłaci 50 złotych polskich. Twórcy zbyt lichych wierszyków zapłacą karę do 10 złotych". Redakcja "Parametru" niezwłocznie zwróciła się do pana Cwojdzińskiego z żądaniem wypłacenia 10 złotych.
Najwspanialszym osiągnięciem w tej dyscyplinie jest chyba opowiadanie Michaela Keitha, opublikowane w 1986 roku w magazynie "The Mathematical Intelligencer". Daje ono rozwinięcie dziesiętne liczby π aż do 402. miejsca po przecinku. Redaktorzy pisma, zachęcając do ułożenia jeszcze dłuższego tekstu, ostrzegają przed miejscem 601., gdzie pojawiają się trzy kolejne zera (zera w pi-ematach są oznaczane znakami przestankowymi różnymi od kropki), oraz przed miejscem 772. - tam znajduje się z rzędu sześć dziewiątek i ósemka.
W Księdze rekordów Guinnessa figuruje Japończyk Haraguchi Akira, który w 16 godzin wyrecytował 100 000 cyfr. Polacy w tej dyscyplinie dopiero stawiają pierwsze kroki. W 2014 roku w konkursie na Politechnice Krakowskiej wygrał student budownictwa na tej uczelni - Dawid Wójcik, który wyrecytował z pamięci 1954 cyfry π. - Nie ma się czym chwalić. Wystarczy ćwiczyć pamięć od dziecka. Zapamiętanie wszystkich cyfr zajęło mi kilka dni, tuż przed konkursem - mówił skromni.
NIESAMOWITA LICZBA π
Jeśli chcesz sprawdzić, gdzie w rozwinięciu liczby π występuje np. Twoja data urodzenia, zajrzyj na stronę, gdzie opublikowano pierwszy milion cyfr tego rozwinięcia:
http://www.314159265358979323846264338327950288419716939937510582097494459.comMoże zrobić to za Ciebie komputer na stronie: http://www.facade.com/legacy/amiinpi
JAK BRZMI LICZBA π?
Jeśli chcesz posłuchać liczby π, wiedząc, że każdej cyfrze odpowiada pewna wysokość (częstotliwość) dźwięku, to melodii wygrywanej przez kolejne cyfry rozwinięcia π możesz posłuchać na stronie: https://youtu.be/wK7tq7L0N8E lub https://youtu.be/OMq9he-5HUU





